Reconstructing Antimatter Falling at CERN
Status Update
This page is currently pretty dated, and I’ll update it when I have the chance but for now see arXiv paper.
TL;DR
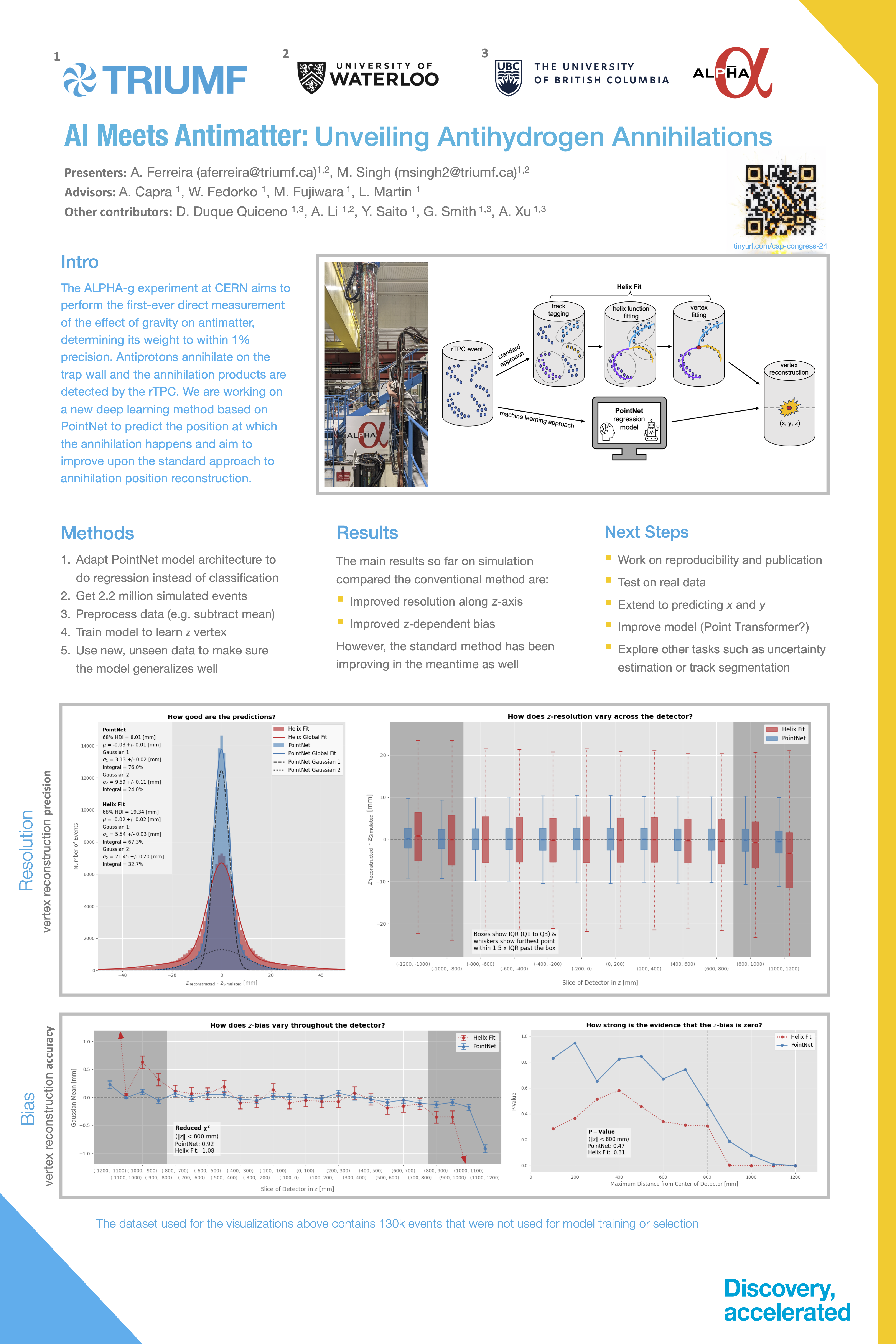
Reconstructing antimatter events with Machine Learning (ML) is a relatively untouched approach and my work has shown it to be viable using simulations from the leading experiment located at CERN.
Built With
Background
Antimatter is similar to normal matter but has the opposite charge and is much more rare. When a particle and its antiparticle meet, they annihilate, so the fact that the universe seems to be dominated by matter is not well understood since equal amounts of matter and antimatter are thought to have been produced during the Big Bang. Some of the most compelling theories to explain this suggest that matter and antimatter must react differently to a force like gravity.
ALPHA is a leading experiment in the study of antimatter, with a track record of publishing major breakthroughs in Nature. The most recent of which was Observation of the effect of gravity on the motion of antimatter in September 2023 which detailed the first-ever measurements of the effect of gravity on antimatter, providing that it does fall down, and not up, but leaving large uncertainties ranges that necessitate antimatter be measured further before it can be said if gravity effects a particle and its antiparticle differently.
This is super preliminary and in-progress work from the summer of 2023 and now that I am back on this project we have been able to dramatically increase the resolution and lower the z-dependant bias of the model such that it is beating the conventional method and has the potential to be used for real physics analysis.
Goal
ML-based event reconstruction may be one way to lower these uncertainty bounds and so the goal of this project is to create a ML model that predicts the annihilation positions of antihydrogen for the ALPHA-g antimatter experiment at CERN.
Currently, the model is trained on simulations but the plan is to adapt it to real data in the future.
Method
Method used is a fully-supervised implementation of PointNet: 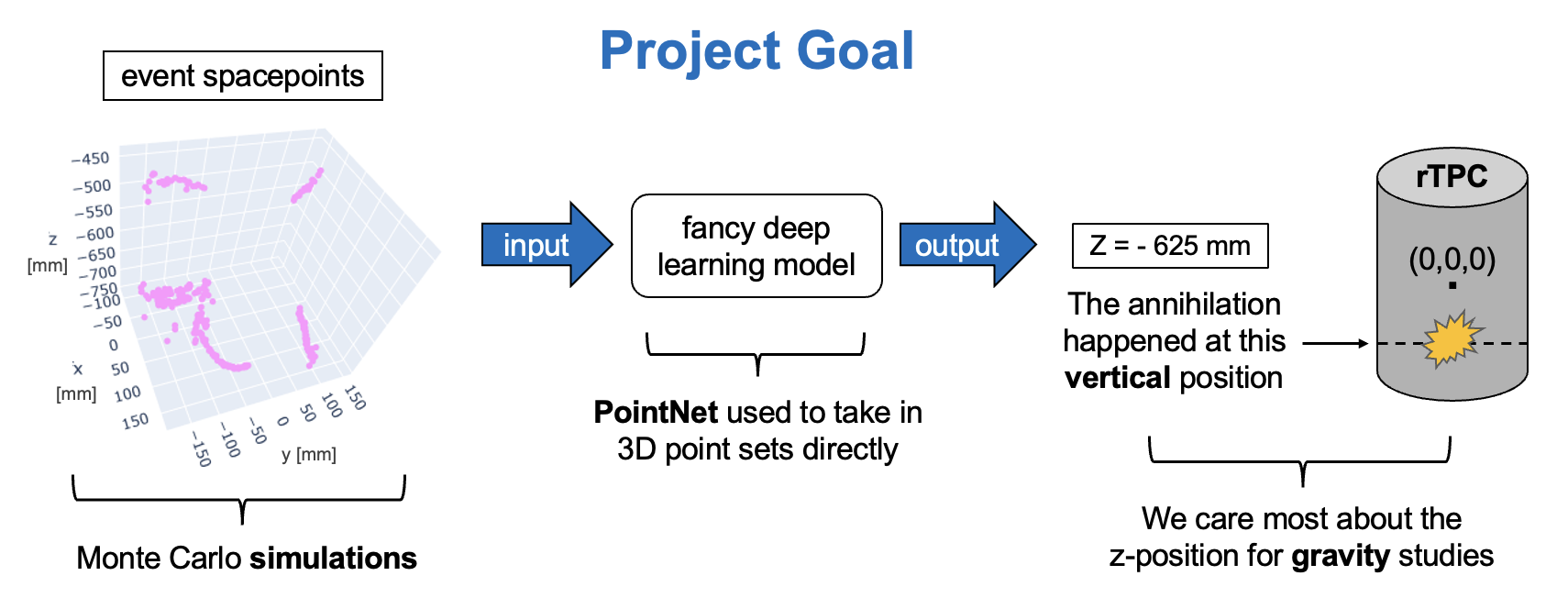
And the goal is that this can replace the existing “Helix Fit” method: 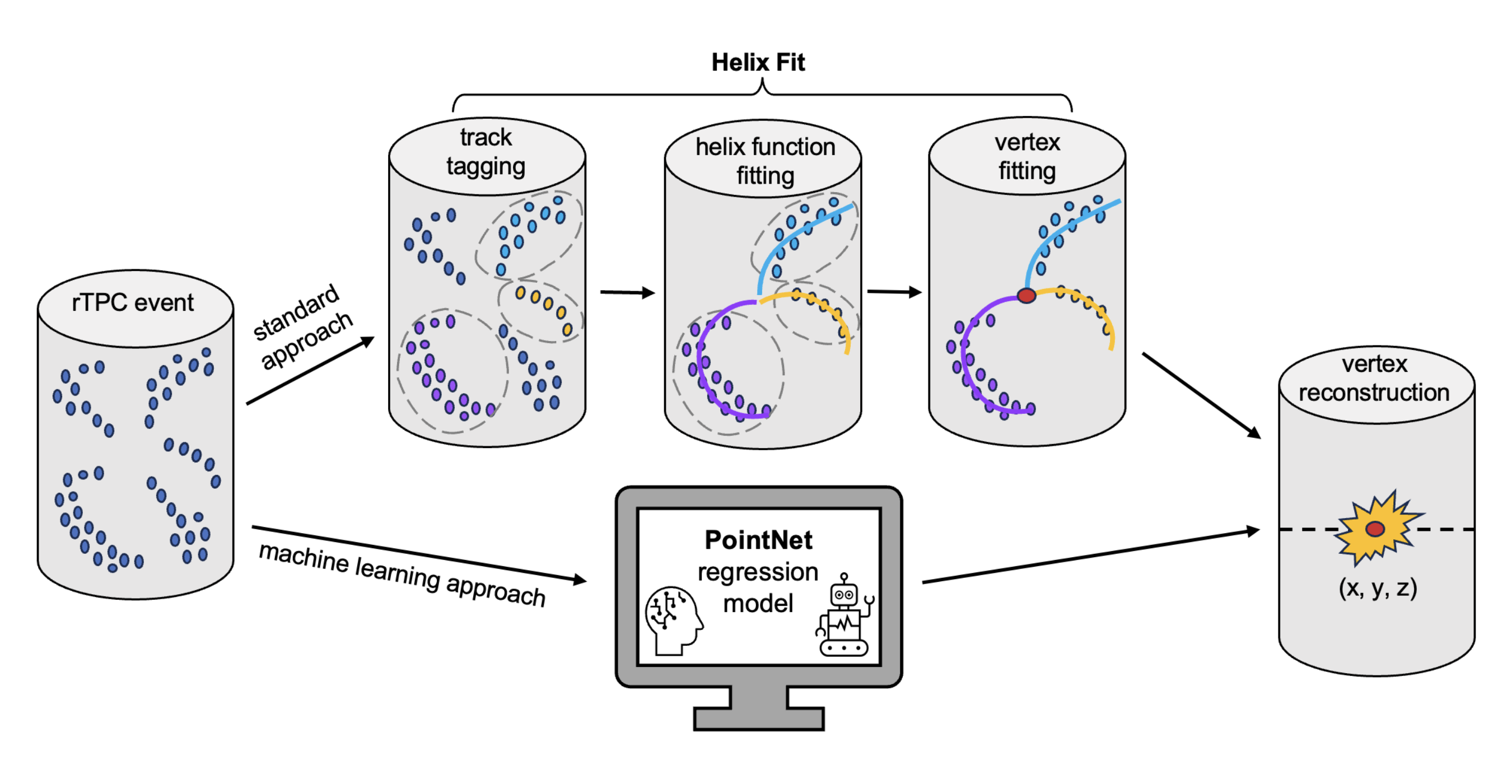
Results
Our results are constantly improving these days but generally, we take the unnormalized predictions and comparing them to the known real z values. They are shown to have a really strong correlation:
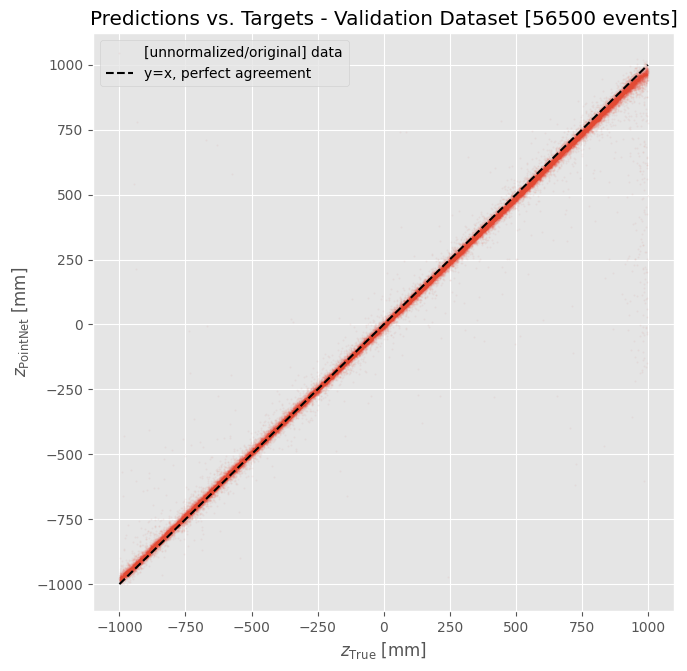
And a more granular way of analyzing this plot is by calculating the residuals, throwing those on a histogram, and doing a guassian fit:
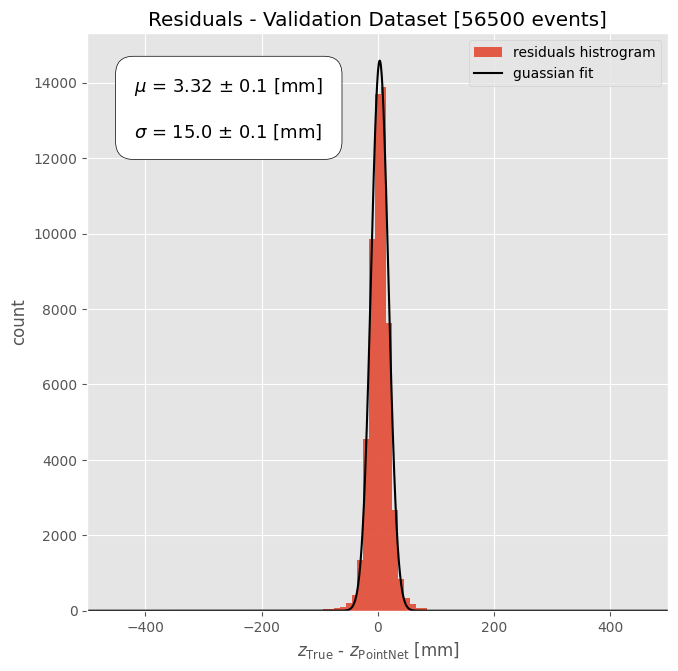
The good news about this plot is it means in the majority of cases, the predicted z value of annihilation is within 15 mm of the real z position of annihilation. The bad news is that these results still lag behind the traditional computational method and so more work was needed for the ML method to beat and not just compliment, or backup, the traditional method.
That has been thoroughly achieved now though, with the ML method having significantly better resolution than the conventional method: 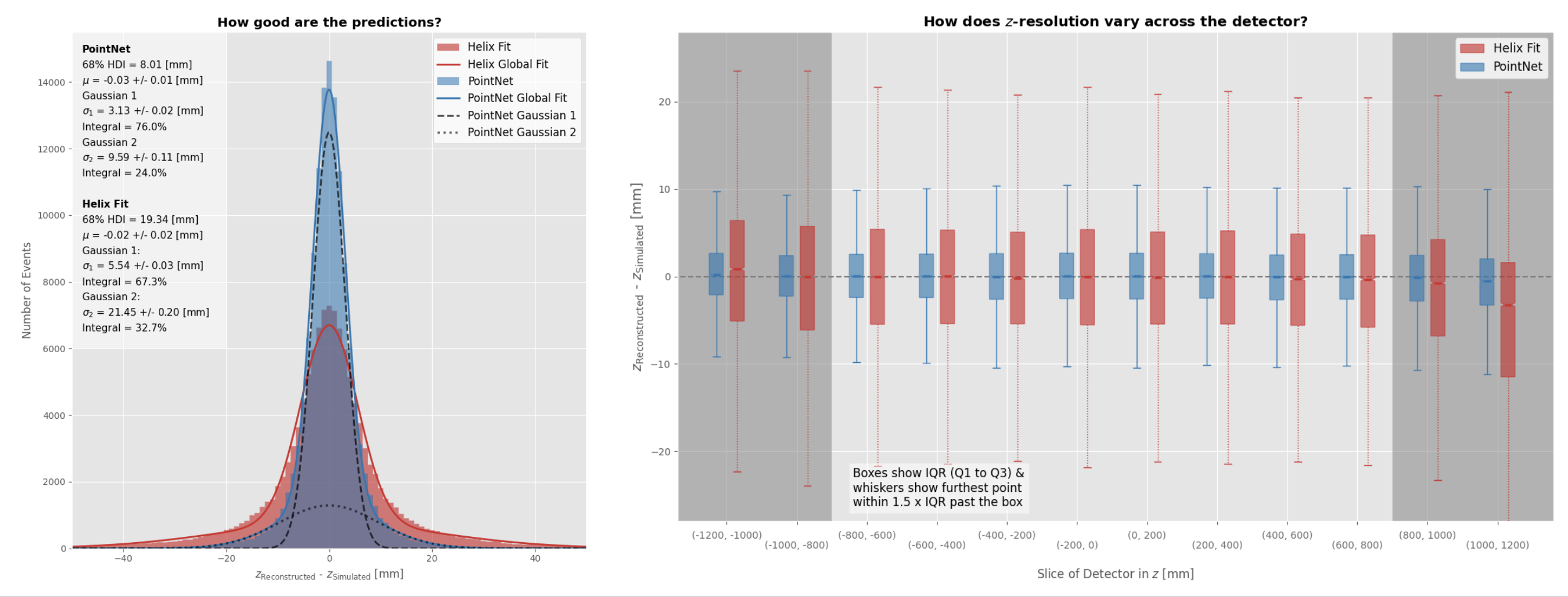
And finally, we deeply care about z-dependant bias as this is a scientific experiment where all contributions of systematic bias need to be as low as possible. This bias is something the ML method struggled with for a long time but that recently has been solved: 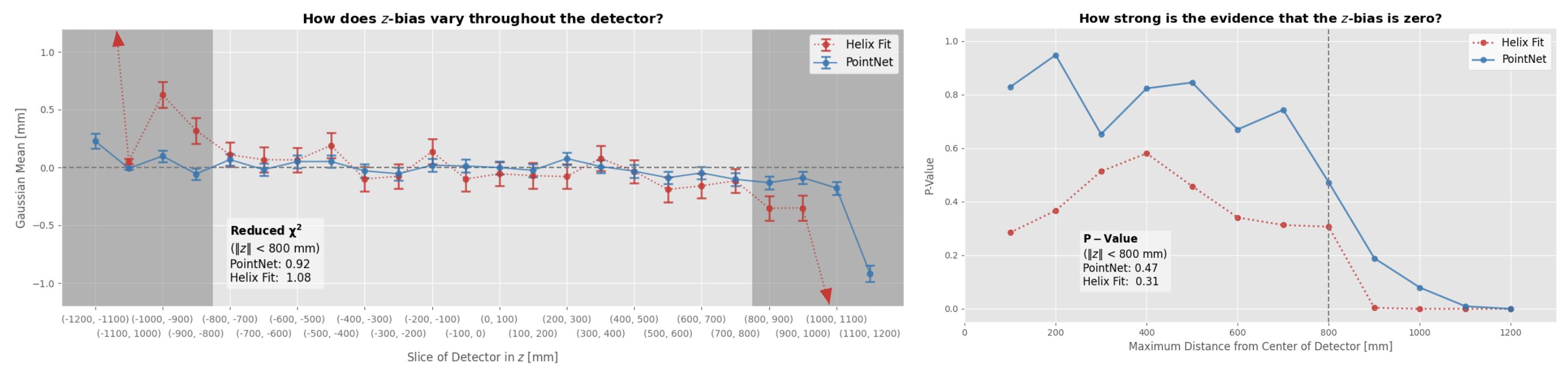
We are also now working on predicting x and y so that we have the full set of cartesian coordinates (x,y,z) and are currently significantly beating the conventional method on every axis.
Conclusion
These results are very promising! Good enough that this model will likely be used in actual analysis some day which is very exciting to me.
A unsolved problem for this work is accurate uncertainty and/or confidence qualification for the predictions. Currently, I am experimenting with some ensemble-based methods and they seem to be very useful for providing a confidence threshold that we can apply a cut on to filter out really bad resolution events to have a clean sample of predictions. This method is able to dynamically estimate uncertainties in a way that is more accurate than using general statistics from the testing analysis and more transferable to real data, however this is still in need of improvement before it can be implemented.
Resources
- Code is currently available through the internal TRIUMF GitLab and will hopefully be made publicly available: